Behler-Parrinello Potential
The Behler-Parrinello potential is a type of machine learning potential that uses explicit features to represent the local atomic environment. It was one of the first MLPs to be developed and is widely used in the field of computational chemistry and materials science. The Behler-Parrinello potential uses atomic-centered symmetry functions (ACSFs) as explicit features, which are designed to be invariant to atomic permutation, translation, and rotation. The ACSFs are then used as input to a feed-forward neural network (NN) model to predict the potential energy of the system.
Total Energy¶
The main idea is to decompose the total energy of a system into contributions from individual atoms, which are then represented by the ACSFs.
Symmetry Functions¶
where is the energy contribution from atom and is the total number of atoms in the system. The ACSFs are constructed based on the distances and angles between the target atom and its neighbors, capturing the local environment around each atom.
where is the radial symmetry function for atom , is the distance between atoms and , η is a width parameter that controls the sensitivity of the function, and is a cutoff function that ensures the symmetry function only considers neighbors within a certain distance:
where is the cutoff distance. The radial symmetry functions capture the distances between the target atom and its neighbors, providing information about the local environment.
The angular symmetry functions () are constructed by:
where is the angle between the bonds connecting atom to atoms and , ζ is a parameter that controls the sensitivity of the function, and λ is a parameter that determines the weight of the angular contribution. The angular symmetry functions capture the angles between the target atom and its neighbors, providing additional information about the local environment.
Neural Network¶
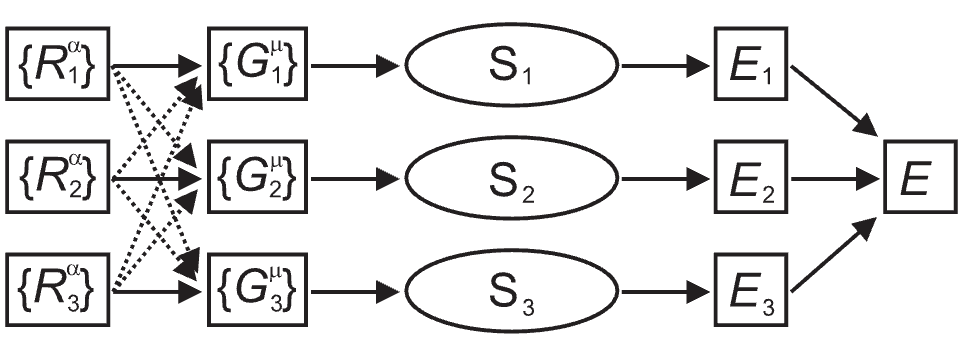
Structure of the neural network of the Behler-Parrinello potential containing 3 atoms. The Cartesian coordinates of atom are represented by and then trensformed to a set of symmetry function values . The symmetry function is then passed to a subnet to compute atomic energy and the total energy is obtained by summing over all atomic energies.
Performance¶
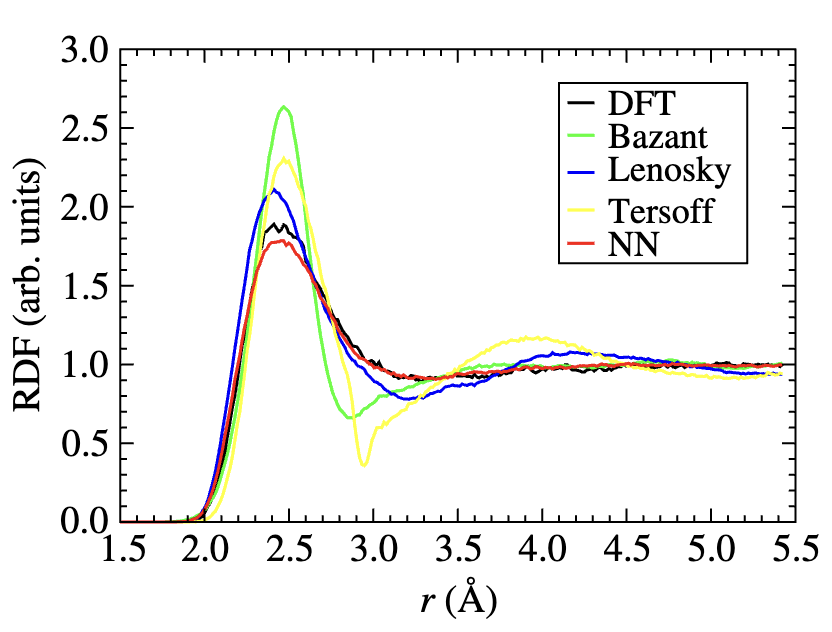
Radial distribution function (RDF) of Si melt at 3000 K. The RDF is calculated using the Behler-Parrinello potential and compared with the RDF obtained from first-principles calculations and other force fields. The agreement between the two RDFs indicates that the Behler-Parrinello potential accurately captures the local atomic environment in the Si melt.
The Behler-Parrinello potential has been shown to provide accurate predictions of the potential energy surface for a wide range of materials and systems, including metals, semiconductors, and biomolecules. It is particularly effective for systems with complex bonding environments, such as transition metals and alloys. The potential is also able to capture the effects of long-range interactions and can be used to model systems with varying atomic coordination numbers.
- Behler, J., & Parrinello, M. (2007). Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces. Physical Review Letters, 98(14). 10.1103/physrevlett.98.146401