Choose an Optimization Algorithm
When choosing an optimization algorithm, it is important to consider the computational cost of calculating the objective function and its derivatives. Some methods, such as Newton’s method, require second derivatives, which can be expensive to compute.
The size and dimensionality of the problem can significantly impact the performance of different algorithms. For high-dimensional problems, methods like L-BFGS, which use limited memory, may be more suitable.
Different problems may respond better to different algorithms and parameter settings. Therefore, it is crucial to experiment with various methods and tune parameters, such as the learning rate in gradient descent, to find the most effective approach.
Visualizing the results is essential to ensure that the algorithm is converging and the solution is reasonable. This can help identify issues such as poor convergence or getting stuck in local minima.
For global optimization, the choice of algorithm depends on the properties of the objective function. For noisy objective functions, simulated annealing is a good choice. When dealing with discrete variables, a genetic algorithm is suitable. If the computational cost is high, basin hopping can be used.
No Free Lunch Theorem¶
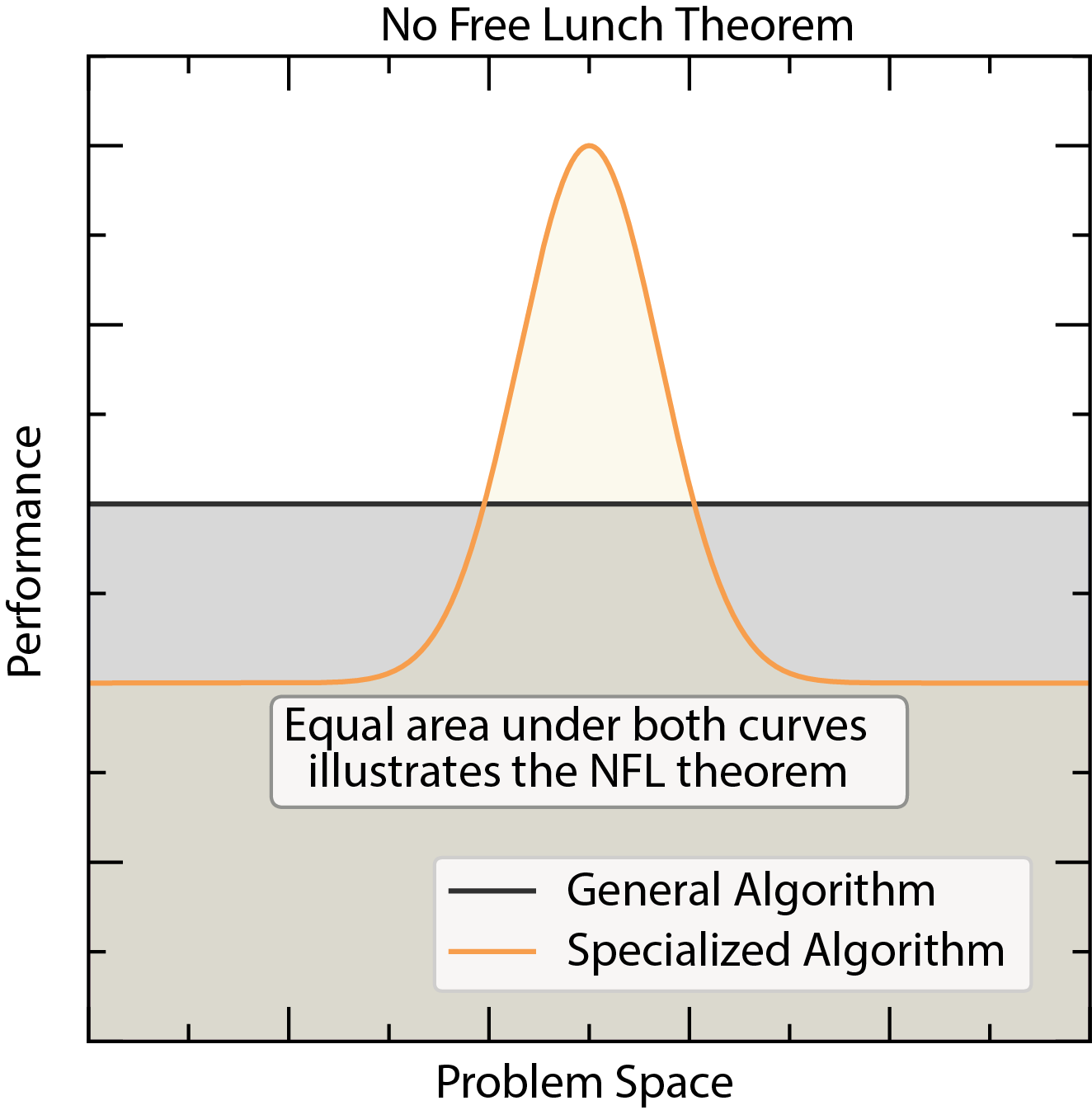
No Free Lunch Theorem: No single optimization algorithm is the best for all problems.
The “No Free Lunch” theorem in optimization states that no single optimization algorithm is the best for all problems. The performance of an algorithm depends on the specific properties of the problem. Therefore, it is essential to understand the characteristics of the optimization problem and choose an algorithm that is well-suited to those properties.