Noncrystalline Materials
Noncrystalline materials, also known as amorphous materials, lack the long-range order that is characteristic of crystalline materials. This lack of long-range order is due to the absence of a repeating unit cell, which is a defining feature of crystalline materials. Noncrystalline materials are characterized by a disordered atomic structure that does not exhibit the periodicity of a crystal lattice. This disordered atomic structure gives rise to unique properties and behaviors that distinguish noncrystalline materials from their crystalline counterparts.
Radial Distribution Function (RDF)¶
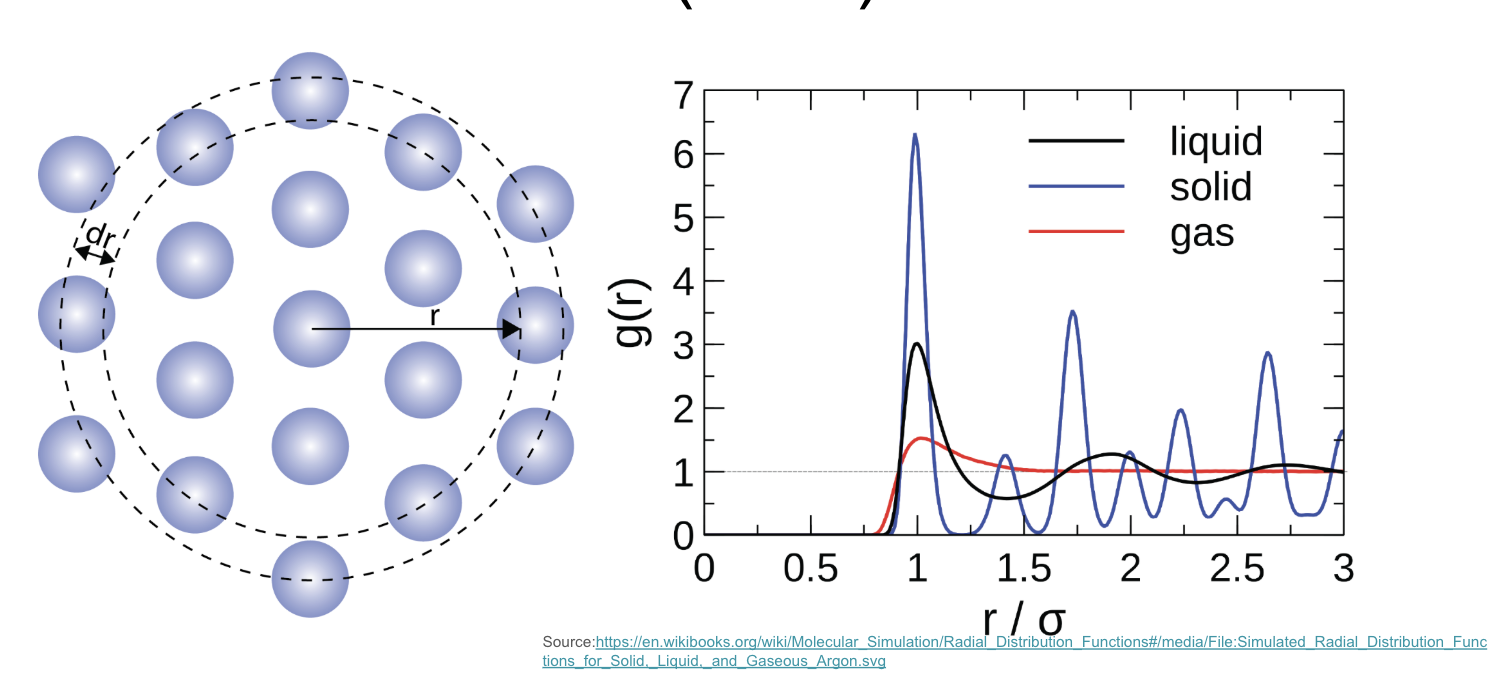
Radial Distribution Function (RDF) and examples of solid, liquid, and gas RDFs.
In the absence of long-range order, non-crystalline materials exhibit short-range order (SRO) within a limited range (0 ~ 5 Å). Due to the lack of translational symmetry, describing the atomic positions throughout the entire structure becomes challenging. The radial distribution function (RDF), denoted as g(r), offers a statistical approach to characterize the atomic arrangement.
The RDF, g(r), quantifies the probability of finding an atom at a specific distance, r, from a reference atom. In essence, it describes how the atomic density varies as a function of distance from a chosen atom. Experimentally, the RDF can be obtained from scattering techniques, such as X-ray or neutron diffraction, as it is directly related to the structure factor S(q).
The shape of the RDF provides valuable insights into the material’s structure. Crystalline materials, with their well-defined atomic positions, exhibit sharp peaks in the RDF, corresponding to specific interatomic distances. In contrast, non-crystalline materials, liquids, and gases display broader peaks, reflecting the inherent disorder in their atomic arrangements. In the limiting case of an ideal gas, where atoms are randomly distributed, the RDF approaches unity (g(r) = 1), indicating a uniform probability of finding an atom at any distance.