Software
Software is very important for computers, and in this section, we will dive into software and understand how it works on a computer.
Firmware, often referred to as BIOS (Basic Input/Output System), plays a crucial role in booting up a computer system. It initializes the hardware components and loads the operating system, providing low-level control over various devices. Without firmware, the computer would not be able to start or function properly.
The operating system (OS) is the backbone of any computer system, managing both hardware and software resources. It handles processes, manages the filesystem, and oversees input/output (I/O) operations. The OS ensures that different programs and users running on the computer do not interfere with each other, providing a stable and efficient environment for applications to run.
Applications are software programs that run on top of the operating system, allowing users to perform specific tasks. These tasks can range from word processing and web browsing to complex data analysis and graphic design. Applications interact with the hardware through the OS, making it possible for users to leverage the full capabilities of their computer systems to accomplish their goals.
Programming Languages¶
Programming languages are used to create software. Popular programming languages in scientific computing include Python, C/C++, and Fortran. C/C++ and Fortran need to be compiled before execution, whereas Python uses an interpreter to execute the code line by line. Python is highly extensible by importing modules. Useful packages include numpy, scipy, and matplotlib. Although Python is much slower than C/C++ and Fortran, it can take advantage of numerical libraries such as numpy, which uses fast numerical libraries like BLAS and LAPACK for high performance.
Libraries¶
Software libraries are like toolkits filled with pre-written code that help you perform specific tasks without starting from scratch. Think of them as shortcuts that save you time and effort. They come with functions and classes that you can call through an application programming interface (API). Since these libraries are tested by experts and the community, they are reliable and efficient. Using these libraries means you don’t have to reinvent the wheel, allowing you to focus on solving your specific problems more effectively.
In scientific computing, several libraries are commonly used:
BLAS (Basic Linear Algebra Subprograms): Provides low-level routines forlinear algebra operations, such as matrix multiplication and vector addition.
LAPACK (Linear Algebra Package): Built on top of BLAS, offers higher-levellinear algebra operations like matrix diagonalization and solving linear systems.
ScaLAPACK (Scalable LAPACK): Extends LAPACK for distributed memory systems,performing linear algebra calculations across multiple processors.
FFTW (Fast Fourier Transform in the West): Used for computing discreteFourier transformations, which are essential in signal processing.
OpenMPI: An open-source library for message passing, crucial for parallel computing, allowing different parts of a program to communicate with each other efficiently.
Scaling¶
In materials science, problems often involve handling large amounts of data, such as information about atoms and their interactions. Understanding the efficiency of algorithms is crucial when dealing with such data-intensive tasks. This efficiency is often described using Big O notation, which classifies algorithms based on their time complexity. Understanding these different types of scaling helps in selecting the appropriate algorithms and optimizing performance for various computational tasks in materials science.
For example, accessing an array element by its index is an operation that takes constant time, denoted as O(1). This means the time required to perform the operation does not depend on the size of the array.
Linear scaling, represented as O(N), occurs when the time required to complete a task grows directly in proportion to the size of the input data. An example of this is iterating through a list or reading a file line by line.
Quadratic scaling, or O(), happens when the time required grows with the square of the input size. This is common in tasks involving nested loops, such as molecular-level simulations.
Polynomial scaling, such as O(), is seen in more complex operations like matrix multiplication, diagonalization, inversion, and calculating determinants, which are often encountered in quantum mechanics.
Logarithmic scaling, denoted as O(N log N), is typical for algorithms like the Fast Fourier Transform (FFT), which is used in signal processing and other applications.
Exponential scaling, represented as O(), occurs in algorithms that solve problems recursively or involve combinatorial tasks. These algorithms can become impractical for large input sizes due to their rapidly increasing time requirements.
Parallel Computing¶
Modern computers are equipped with multiple processors or cores, allowing them to perform parallel computing. This means that tasks can be divided into smaller sub-tasks and executed simultaneously across different processors, significantly reducing the overall execution time. The concept of parallel computing is essential for handling large-scale computations efficiently.
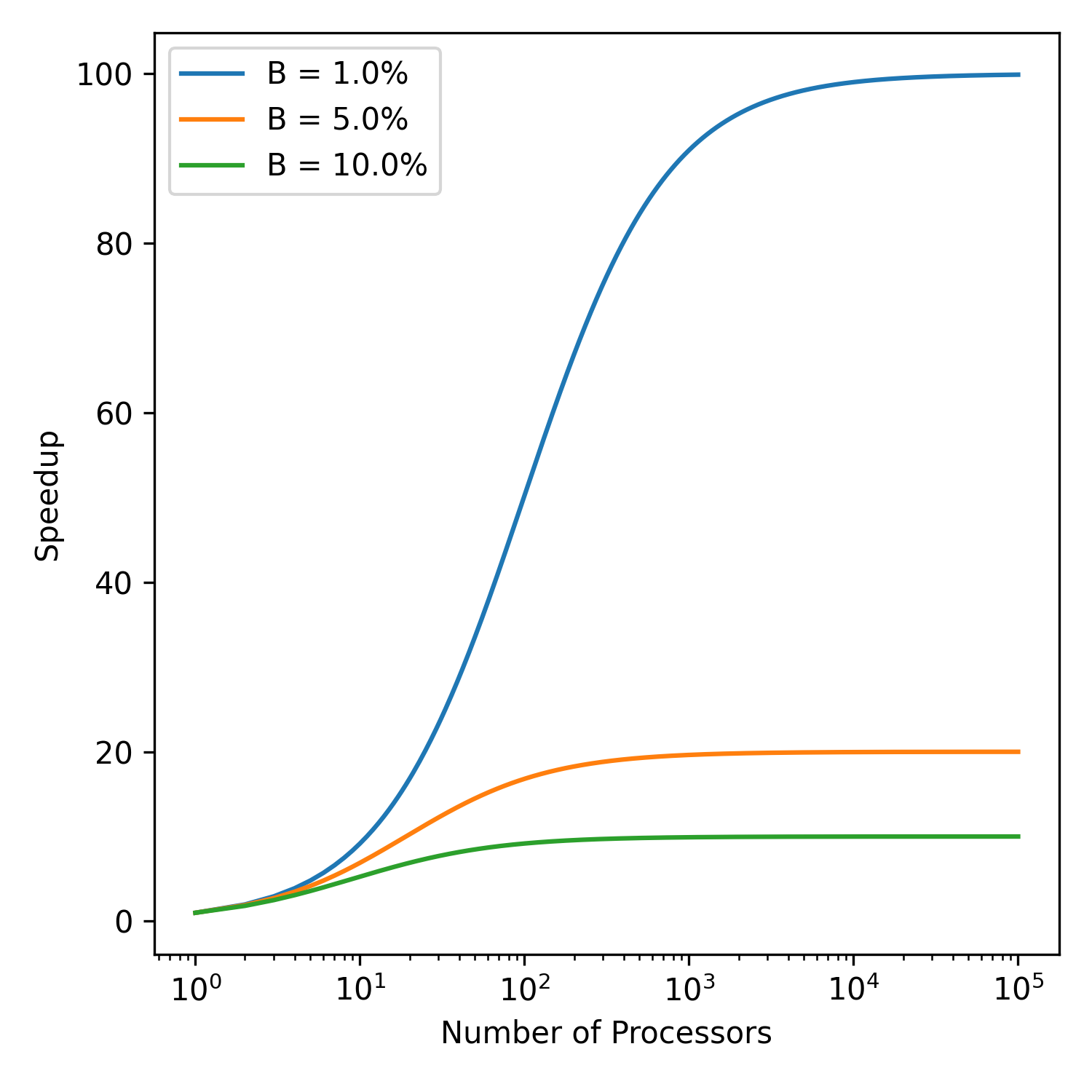
The speed up of a parallel code can be estimated using the Amdahl’s law.
One way to estimate the potential speedup of parallel code is by using Amdahl’s Law. Amdahl’s Law provides a formula to calculate the theoretical maximum speedup of a program when only a portion of it can be parallelized. The formula is given by:
In this equation, S represents the speedup, N is the number of processors, and B is the fraction of the code that is executed serially (i.e., cannot be parallelized). According to Amdahl’s Law, the speedup is limited by the serial portion of the code. If a significant part of the code must be executed serially, achieving substantial speedup becomes challenging, even with a large number of processors.
For instance, if B is not very small, it becomes difficult to fully utilize a system with many cores. This is because the serial portion of the code creates a bottleneck, preventing the program from achieving maximum parallel efficiency. Additionally, communication between processors can further reduce scalability. When processors need to exchange information frequently, the overhead from communication can also negate the benefits of parallel execution.
To maximizethe benefits of parallel computing, it is crucial to minimize the serial portion of the code and optimize communication between processors. Techniques such as load balancing, minimizing data dependencies, and using efficient communication protocols can help improve the performance of parallel programs.