Unit Cell
In crystalline materials, atoms are arranged in a regular, repeating pattern that extends in three dimensions. This orderly arrangement forms what we call a crystal lattice. To understand and analyze these complex structures, we need a way to represent them simply and efficiently.
A unit cell serves as the smallest repeating unit that shows the full symmetry of a crystal structure. By replicating this unit cell in three dimensions, we can reconstruct the entire crystal lattice. The unit cell’s dimensions are defined by three lattice vectors, which represent the crystal’s periodicity in each direction.
Lattice Vectors¶
The unit cell’s dimensions are defined by three lattice vectors, , , and . These vectors represent the crystal’s periodicity in each direction and define the unit cell’s shape and size.
These vectors can be organized into a matrix form, known as the lattice matrix:
where 1, 2, and 3 represent the x, y, and z components of the lattice vectors, respectively. The length of lattice vectors are called lattice constants, denoted as , , and . The angles between the lattice vectors are denoted as α, β, and γ. The lattice vectors are typically chosen to be orthogonal, with angles of 90 degrees.
Crystal Directions and Planes¶
In crystallography, we use crystal directions and planes to describe the orientation of atoms in a crystal lattice. These directions and planes are defined relative to the lattice vectors , , and .
Any position in the crystal lattice can be expressed as a linear combination of these lattice vectors. For example, a point in the crystal lattice can be written as:
where u, v, and w are integers representing the periodic repetition of the unit cell.
Crystal directions are defined by their indices [uvw], which represent the direction of the vector in terms of the lattice vectors. The indices are enclosed in square brackets and written as [uvw]. For example, the [100] direction is parallel to the lattice vector .
A group of directions that are equivalent due to the crystal’s symmetry is called a direction family <uvw>. For example, the [100], [010], and [001] directions are all part of the <100> direction family.
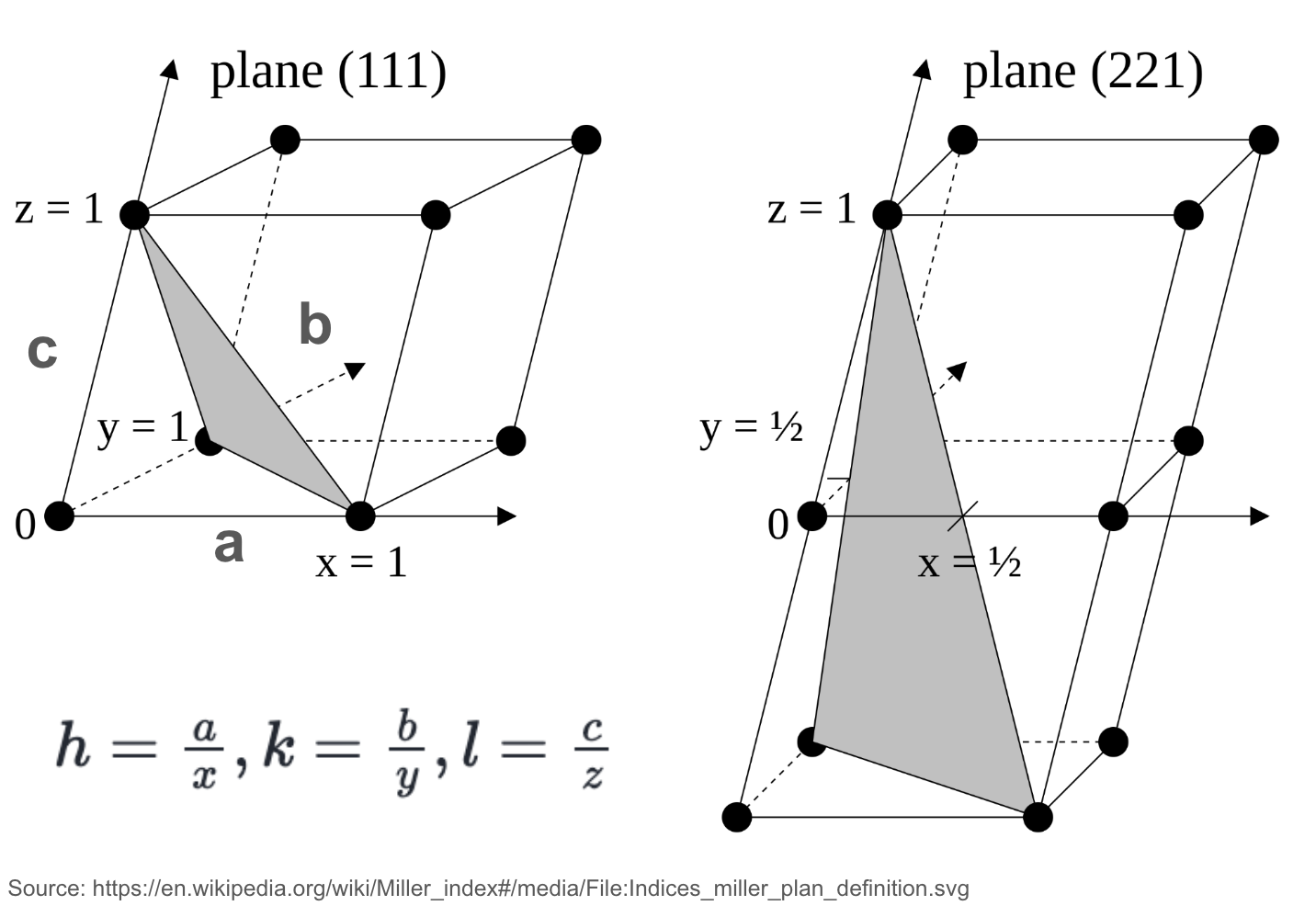
An illustration of crystal directions and planes using the Miller indices notation.
A set of crystallographic planes can be defined by their Miller indices (hkl), which are reciprocals of the intercepts of the plane with the unit cell axes. For a plane with intercepts , , and along the lattice vectors , , and respectively:
where , , and are the lattice constants. These indices (h, k, l) are typically reduced to the smallest set of integers by multiplication or division.
Similarly, a group of planes that are equivalent due to the crystal’s symmetry is called a plane family {hkl}. For example, the (100), (010), and (001) planes are all part of the {100} plane family.
Miller indices are important for interplane spacing, which is the key to understanding diffraction patterns. The spacing between planes is inversely proportional to the square root of the sum of the squares of the Miller indices.
Crystal Systems¶
There are 7 crystal systems in 3D space, which are classified based on the lengths and angles of the edges of the unit cell. The crystal systems are characterized as the table below.
Bravais Lattice¶
Summary of 7 crystal systems and 14 Bravais lattices:
| Crystal System | Bravais Lattices | Lattice Parameters |
|---|---|---|
| Cubic | Simple (P), Body-Centered (I), Face-Centered (F) | |
| Tetragonal | Simple (P), Body-Centered (I) | |
| Orthorhombic | Simple (P), Body-Centered (I), Face-Centered (F), Base-Centered (A,B,C) | |
| Hexagonal | Simple (P) | |
| Trigonal (Rhombohedral) | Rhombohedral (R) | |
| Monoclinic | Simple (P), Base-Centered (A,B,C) | |
| Triclinic | Simple (P) |
Each Bravais lattice represents a distinct 3D periodic arrangement of points in space.
Primitive vs Conventional Unit Cells¶
The primitive unit cell contains exactly one lattice point per cell and has the smallest possible volume. While it is mathematically elegant, it often doesn’t clearly show the crystal’s symmetry. In crystallographic notation, it is denoted by ‘P’.
The conventional unit cell may contain more than one lattice point and is larger than the primitive cell. It better displays the crystal’s symmetry and is commonly used in crystallography. Conventional unit cells can be body-centered (denoted as I), face-centered (F), or base-centered (A,B,C).
As an illustration, consider a face-centered cubic (FCC) structure. In this case, the conventional unit cell contains 4 lattice points, while the primitive unit cell contains only 1 lattice point. This demonstrates how conventional cells, though larger, can better represent the structural symmetry of the crystal.
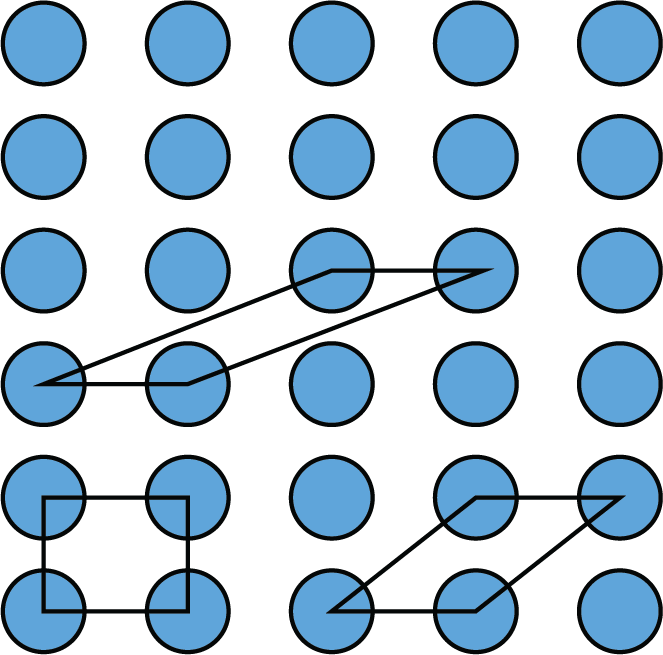
Primitive cell are not unique and can be chosen in different ways. The figure shows three different primitive cells for a lattice.
Choosing a primitive unit cell is not unique, and different choices can be made based on the crystal structure’s symmetry. Niggli reduction is a method to convert a conventional unit cell to a unique primitive unit cell by transforming the lattice vectors to their shortest form. This process simplifies the unit cell representation and makes it easier to analyze the crystal structure.
Crystal Structure¶
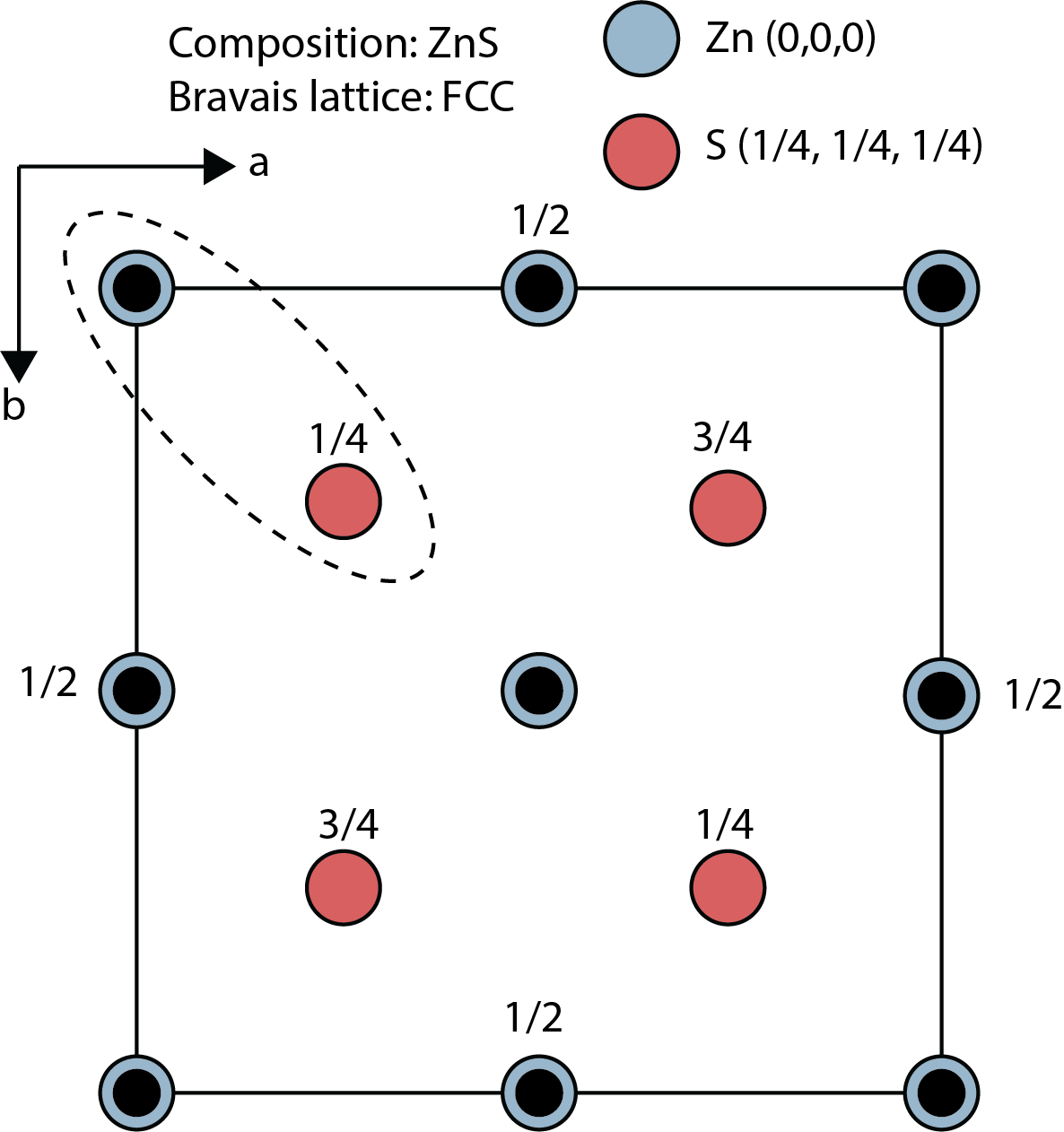
Schematic of a crystal structure with a lattice and motif using a face-centered cubic (FCC) ZnS example. Motif atoms are highlighted in dashed circle.
The crystal structure of a material is defined by the combination of a lattice and a motif. The lattice is a regular, repeating arrangement of points in space, while the motif, or basis, is a set of atoms associated with each lattice point. By placing the motif at every lattice point, we can generate the entire crystal structure. Atoms tend to pack closely together when forming a crystal, minimizing the space between them and creating a dense, orderly structure.