Reciprocal Space
The reciprocal space is a key concept in crystallography and solid-state physics. This space is spanned by reciprocal lattice. It consists of all wave vectors that produce plane waves with the periodicity of a given crystal lattice.
Reciprocal Lattice¶
Given direct lattice vectors a, b, and c, the reciprocal lattice vectors b*, c*, and a* are defined as:
The reciprocal lattice is important because it simplifies the analysis of wave diffraction and electronic band structure in crystals. By considering the periodicity of the crystal lattice, the reciprocal space allows for a more straightforward interpretation of diffraction patterns and electronic properties. It is particularly useful for understanding X-ray diffraction patterns, which help determine the atomic structure of crystals. Bragg’s law, which describes the condition for constructive interference, can be expressed using reciprocal lattice vectors.
Applications of the reciprocal lattice include:
- X-ray Crystallography: Analyzing diffraction patterns to determine atomic structures.
- Electron Diffraction: Investigating surface structures of materials.
- Solid-State Physics: Studying electronic band structures and phonon dispersion relations.
Brillouin Zone¶
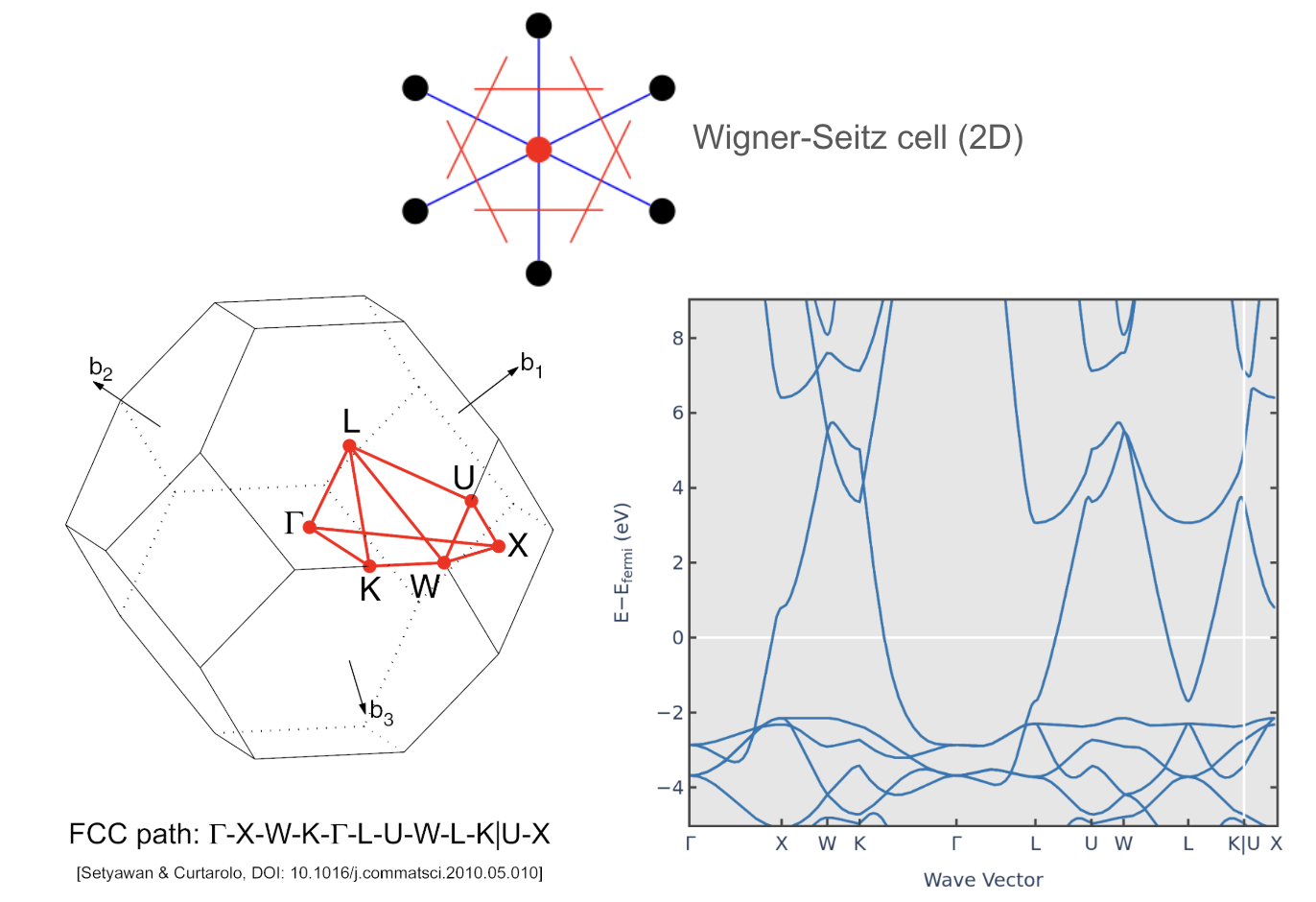
Weigner-Seitz cell in reciprocal space and the first Brillouin zone of an FCC lattice.
The Brillouin zone is a uniquely defined primitive cell in reciprocal space. It is the Wigner-Seitz cell of the reciprocal lattice and is constructed by drawing perpendicular bisectors to the reciprocal lattice vectors from the origin. The first Brillouin zone contains all the unique wave vectors that can be used to describe the periodicity of the crystal.
In a three-dimensional crystal, the Brillouin zone is a polyhedron, and its shape depends on the symmetry of the crystal lattice. For example, in a simple cubic lattice, the first Brillouin zone is a cube, while in a face-centered cubic lattice, it is a truncated octahedron.
The concept of the Brillouin zone is crucial for understanding the electronic properties of solids. It helps in the analysis of electron energy bands and the behavior of electrons in a periodic potential. The boundaries of the Brillouin zone are where Bragg reflection occurs, leading to the formation of energy band gaps.
Key points about the Brillouin zone include:
- It is the fundamental region of the reciprocal space that contains all the distinct wave vectors.
- The first Brillouin zone is the most commonly used, but higher-order zones can also be defined.
- The shape and size of the Brillouin zone are determined by the crystal lattice structure.
- It plays a significant role in the band theory of solids, particularly in the determination of allowed and forbidden energy bands.
Understanding the Brillouin zone is essential for interpreting various phenomena in solid-state physics, such as electrical conductivity, optical properties, and thermal properties of materials.