Graph Neural Networks
Graph Neural Networks (GNNs) are a class of neural networks designed specifically to operate on graph-structured data, such as the atomic graphs we just described. Their core operational principle is typically message passing.
ML Tasks¶
We can do supervised or unsupervised learning with GNNs. In supervised learning, we have a dataset of graphs with known labels (e.g., total energy, band gap) and we want to learn a mapping from the graph structure and features to these labels. In unsupervised learning, we might want to learn useful representations of the graphs without explicit labels, which can be useful for tasks like clustering or anomaly detection.
There are several types of tasks that GNNs can be applied to, depending on the level of granularity at which we want to make predictions:
- Node-level tasks: Predicting properties of individual nodes (e.g., predicting the type of atom based on its local environment).
- Edge-level tasks: Predicting properties of edges (e.g., predicting bond types or distances).
- Graph-level tasks: Predicting properties of the entire graph (e.g., predicting the total energy of a molecule or the band gap of a crystal).
Message Passing¶
Message passing is a mechanism by which nodes in a graph can exchange information with their neighbors. This process allows GNNs to learn representations of nodes based on their local connectivity and features, effectively capturing the graph’s structure and the relationships between its components.
Imagine the atoms within a structure “communicating” with their local environment. In a GNN, this communication occurs iteratively over several layers. Let denote the feature vector (or embedding) of node at layer . The process can be conceptually represented as:
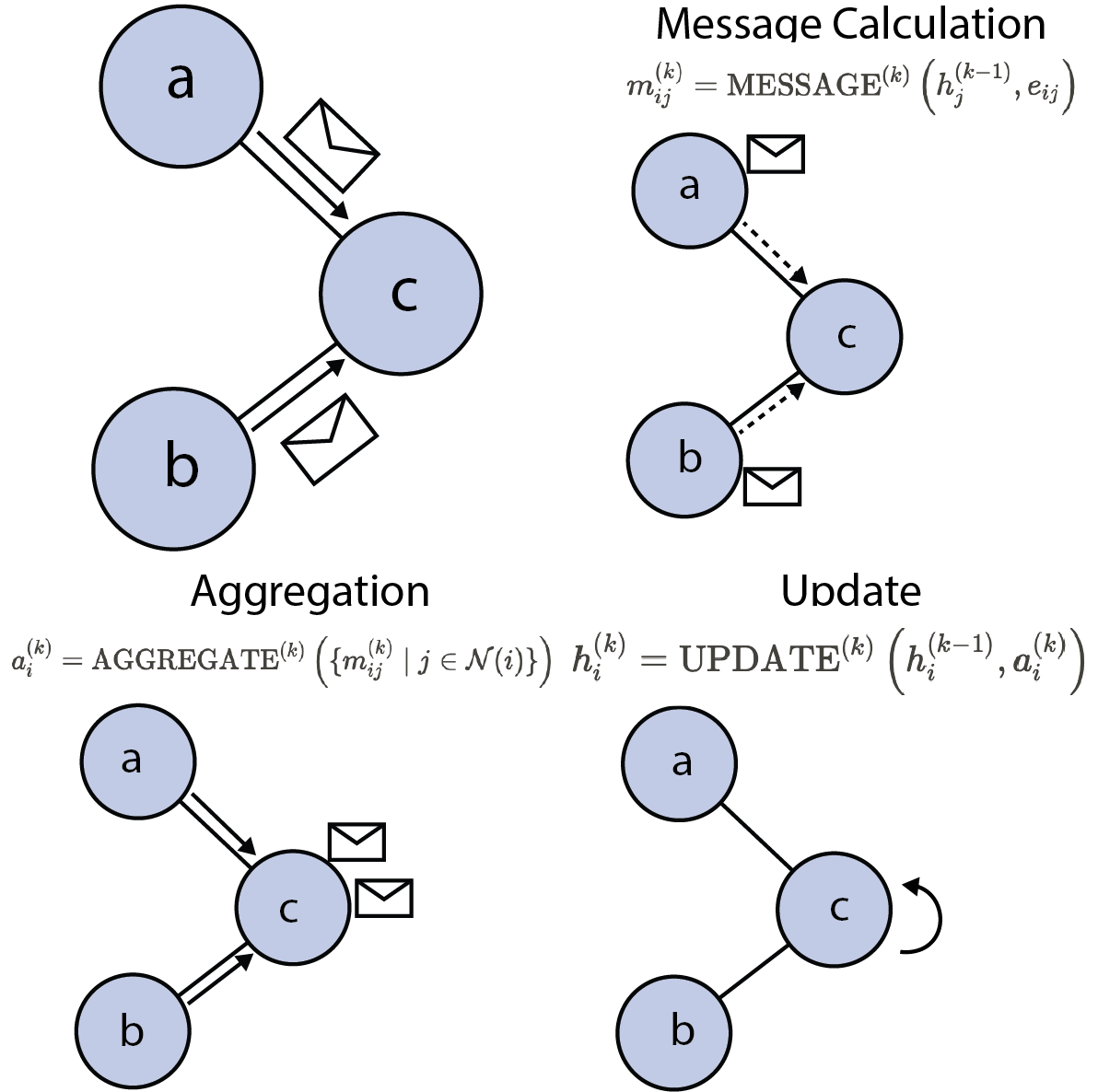
Message passing process in a GNN: message calculation, aggregation, and update steps.
Message Calculation (Optional but common)¶
Transform neighbor features potentially considering edge features . The message from node to node at layer is computed as:
where is the message from node to node at layer . The message function can be a simple linear transformation, a neural network, or any other differentiable function that combines the node features and edge features. This step is optional, as some GNN architectures directly aggregate the node features without explicitly calculating messages.
Aggregation¶
It collects information, or “messages,” from its neighboring nodes (those directly connected by an edge). These messages are typically based on the neighbors’ current feature representations. Common aggregation functions include summation, averaging, or taking the maximum of the incoming message vectors. This step ensures that the node gathers information about its local chemical environment.
where is the set of neighbors of node , and represents the message from to at layer .
Update¶
It updates its own feature vector based on its previously gathered aggregated message and its own feature vector from the previous layer. This update step usually involves a learnable function, often a small neural network, allowing the model to adaptively decide how to integrate the neighborhood information.
Here, AGGREGATE and UPDATE are differentiable functions (often implemented using neural network layers) whose parameters are learned during training. The repeated application of these steps over several layers allows information to propagate across the graph, enabling nodes to incorporate information from beyond their immediate neighbors.
Crucially, because aggregation functions like sum or mean are independent of the order of their inputs, the message passing framework is inherently permutation equivariant at the node level (permuting input nodes permutes the output node embeddings correspondingly) and can be made permutation invariant at the graph level (the overall graph property prediction remains unchanged upon node permutation). This aligns perfectly with the physical requirement that material properties are independent of atom indexing.
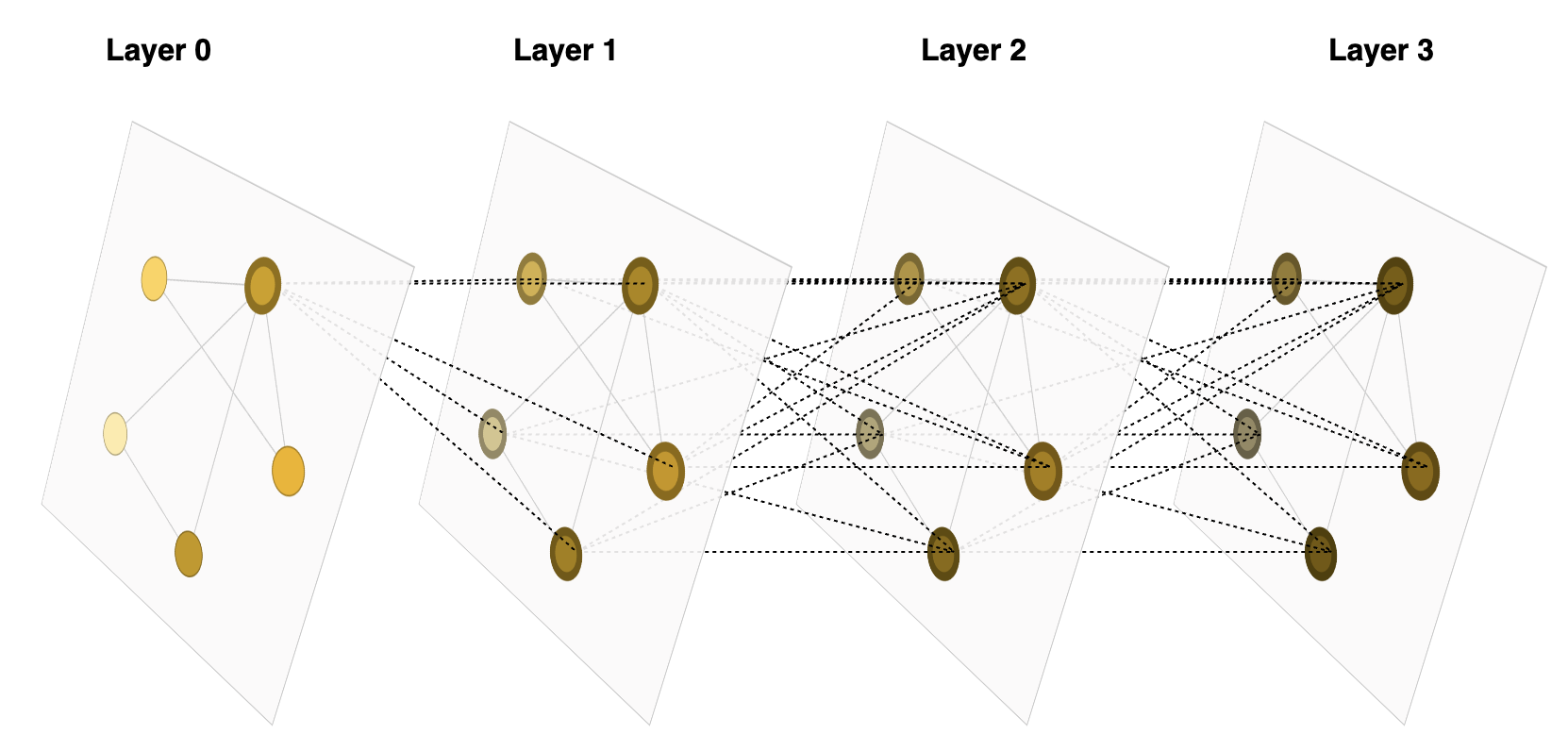
The figure shows the message passing process in a GNN. Each node aggregates messages from its neighbors and updates its own feature vector based on the aggregated information. Figure adapted from A Gentle Introduction to Graph Neural Networks.
Graph-Level Readout¶
After several iterations of message passing, we obtain a set of node embeddings for each node . To make predictions about the entire graph (e.g., predicting the total energy or band gap), we need to aggregate these node embeddings into a single graph-level representation. This is often done using a readout function, which can be as simple as summing or averaging the node features:
where is the graph-level representation. This representation can then be fed into a final prediction layer (e.g., a fully connected layer) to produce the desired output.
Training¶
The training of GNNs typically involves minimizing a loss function that measures the difference between the predicted graph-level properties and the true properties from the training data. This is often done using standard backpropagation techniques, where gradients are computed with respect to the model parameters and updated using an optimization algorithm (e.g., Adam, SGD).
Strengths and Limitations¶
Strengths:
- Directly utilizes atomic structure and connectivity information.
- Inherently handles permutation invariance requirements.
- Effectively captures local chemical environments.
- Adaptable to various graph structures and property prediction tasks.
Limitations:
- Standard message passing can struggle to efficiently capture very long-range interactions within the material (requiring many layers).
- Performance can be sensitive to the choice of graph construction (definition of edges/neighbors).
- Can be computationally more intensive to train and evaluate than simpler descriptor-based models.
- Interpretability – understanding why a GNN makes a specific prediction – remains an active area of research.
- Sanchez-Lengeling, B., Reif, E., Pearce, A., & Wiltschko, A. (2021). A Gentle Introduction to Graph Neural Networks. Distill, 6(8). 10.23915/distill.00033